1차 순열

여기서 말하는 대입은 대입적분을 할 때의 대입과는 완전히 다른 것으로 고등학교 확률통계에서 배운 순열과 같은 의미를 갖는다. 영어 단어는 동일합니다. 순열은 특정 개체를 선택하고 배열하는 것을 말합니다. 이것은 전단사 함수, 즉 일대일 함수로 볼 수 있습니다. 집합 Z에서 자체로의 함수입니다.
위와 같이 행렬로 표현하면 첫 번째 행에는 대입 연산 이전에 본 X의 원소들을 순서대로 적고, 두 번째 행에는 대입에 의해 순서가 바뀐 X의 원소들을 적는다. 행 1은 범위의 요소로 구성되고 행 2는 범위의 요소로 구성되는 것을 볼 수 있습니다. 대체를 두 줄로 표현하면 ‘두 줄 표기법’이라고 합니다. 하지만 첫 번째 행에 X의 원소가 순차적으로 입력되기 때문에 사용하기 싫어서 맨 아래 행만 사용하는 경우가 있습니다. 그런 다음 “한 줄 표기법”에 대해 말합니다. 일부 유형의 대체는 한 줄 표기법으로만 작성된다는 것을 곧 알게 될 것입니다.
또한 마지막 행에는 치환의 본질이 순열의 개념이기 때문에 총 치환 횟수는 항상 원소의 개수로 결정된다는 내용을 담고 있다. 무작위 항목의 총 수는 1에서 nn까지이므로! 가 같으면 치환 횟수도 같다.
예 1) S1과 S2의 모든 대체를 찾습니다.
2가 됩니다! 또는 3! 주다. S2의 모든 대체는 다음과 같습니다.
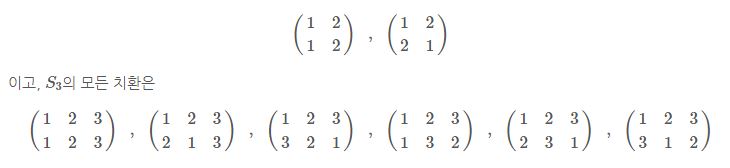
2. 대칭군

치환 합성을 위한 그룹의 세 가지 조건이 충족되면 그룹을 대칭 그룹이라고 합니다. 대칭인 이유는 아래 그림으로 설명하고 먼저 그룹 자체의 조건이 만족되는지 확인합니다. 결국 순열은 전단사 함수이기 때문에 함수의 일종이다. 그러면 일반적으로 함수의 합성 o의 결합법칙이 성립하고 일대일 대응함수는 필연적으로 역함수를 가지므로 역함수가 존재한다. 항등함수는 자신을 대입하는 것으로 군자체의 모든 조건을 만족하는 것으로 동일하고 역대입하는 종류를 정리해 보자.

대칭 그룹은 다음과 같이 실생활에서 발견되는 기하학적 도형의 대칭에서 발견되기 때문에 “대칭”이라고 합니다. B. 예술, 건축 및 수학. 가장 대표적인 것이 삼각형이다.
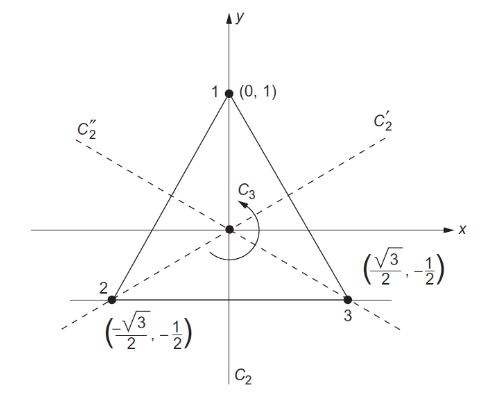
그림과 같이 정삼각형을 회전하거나 뒤집는 방법을 생각해 보십시오. C3는 삼각형의 현재 모양을 유지하기 위한 회전 동작을 말하며 (그림 1)의 위치 (0, 1)에서 세 점 1, 2, 3이 번갈아 나타나도록 하는 변환입니다. 쉽게 말해 120˚(2/3π) 회전(반시계 방향)하는 연산이다. 반면 C2, C2′, C2″는 각각의 축(y축과 점선)을 기준으로 삼각형의 양변을 반전시키는 연산이다.
이때 삼각형의 외형을 유지하는 연산을 상상해 보자. 그러면 6가지가 나옵니다. 삼각형을 그대로 두거나 C3을 회전(120° 회전)하고 C3을 두 번 전진(240° 회전)한 다음 C2, C2′ 및 C2″를 축에 대해 선 대칭으로 회전합니다.
이때 삼각형 1, 2, 3의 각 꼭지점에 번호를 매기고 이들 원소를 원소로 하는 집합의 대입을 고려하면 S3의 원소와 완전히 동일하여 예 1)에서 구하였다.

인정하다. 아래는 순열이 기하학 연산에 어떻게 적용되는지를 보여주는 다이어그램입니다.
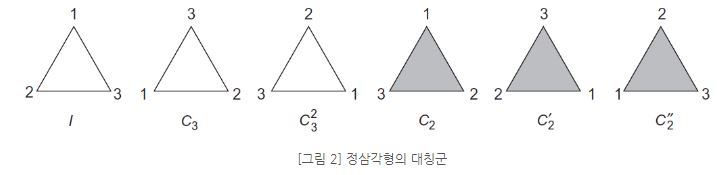
이제 위의 연산으로 꼭지점 수가 변경된 도형과 순열을 나타내는 행렬을 쌍으로 만들어 봅시다. 먼저 6개의 삼각형 중 오른쪽에 있는 3개의 음영 처리된 삼각형을 살펴보겠습니다. 이들은 선대칭(C2)과 관련된 것으로 꼭지점을 지나는 선을 기준으로 양쪽을 반전시켜 수행하는 연산이다. S3에서 이를 나타내는 순열 행렬을 찾으면 순열 관점에서 살펴보겠습니다.
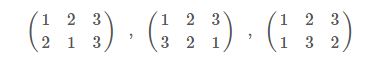
와 동일하며 그 특성은 3원소 중 1원소를 그대로 두고 나머지 2원소를 교환하는 치환에 해당한다.
반면에 왼쪽에 있는 세 개의 삼각형을 고려하십시오. 이들은 회전 작업(C3)과 관련이 있으며 맨 왼쪽에 있습니다. 나는 항등 치환에 의해 삼각형이 변경되지 않은 상태로 유지되는 상황입니다. 두 번째는 120도 회전됩니다. 세 번째는 240도 회전합니다. S3에서 찾으면 어떤 행렬이 될까요?

이 행렬이 됩니다. 이들은 두 개의 반전으로 대체됩니다. 예를 들어 항등행렬은 1과 2를 반전시킨 다음 다시 2와 1을 반전시킨 행렬이고, 두 번째 행렬은 1과 2를 반전시킨 다음 다시 2와 3을 반전시킨 행렬이다. 반면 세 개의 해치가 있는 직각 삼각형인 Chihona는 단일 반전 대체입니다.
이와 같이 대칭이 있는 도형은 대입이라는 연산만 수행하면 여전히 대칭을 유지하며, 정확히는 연산 전후에 모양이 변하지 않으므로 대입으로 이루어진 군을 대칭 군이라고 합니다.
이 예제 도형을 포함하여 일반 n 코너에서 회전 및 미러링 작업을 수행하므로 도형이 교란되지 않으므로 이러한 그룹은 다음과 같은 특수한 경우에 해당됩니다.

예를 들어 괄호 안의 r^n = f^2를 고려하면 n = 3이면 두 번 뒤집으면 시계 반대 방향으로 120˚(2/3π) 회전할 수 있습니다. (그림 2)의 두 번째 삼각형은 120도 회전한 것으로 항등치환에 따라 원래 삼각형에서 1,3, 3,2를 변경한 다음 두 번 반전하여 C3과 동일하게 만들 수 있습니다.
3. 교환법칙
대칭 및 2면체 그룹에는 교환법칙과 관련된 두 가지 정리가 있습니다.

엄밀하게 증명하는 것보다 반례를 통해 이 두 가지 정리가 거짓임을 증명하는 것이 더 적절합니다.

