문제 연결
https://school.programmers.co.kr/learn/courses/30/lessons/161989
프로그램 제작자
코드 중심 개발자를 고용하십시오. 배치 기반 위치 매칭. 프로그래머의 개발자별 프로필에 가입하고 기술 호환성이 좋은 회사와 연결하십시오.
Programmer.co.kr
코딩 테스트 실습 > 실습 > 칠하기
문제 설명
페인트의 길이는 학교에 적용되었습니다 길이가 n 미터인 벽이 있습니다. 벽에 동호회 광고 포스터나 기업 채용 포스터를 붙이기 위해 테이프로 붙였다가 철거하는 과정에서 벗겨지는 경우가 많다. 벽의 벗겨진 페인트가 보기 흉해서 학교는 벽을 다시 칠하기로 결정했습니다.
큰 벽 전체를 다시 칠하는 것보다 벽을 잘라내고 일부만 다시 칠함으로써 비용을 절약할 수 있습니다. 이를 위해 벽을 1미터 길이의 섹션으로 나눕니다. n으로 나누고 각 구역은 왼쪽부터 1번으로 번호가 매겨집니다. 그런 다음 그는 다시 칠해야 할 영역을 식별했습니다.
벽을 칠하는 롤러의 길이 미터, 벽에 롤러로 페인트 한 번 페인팅 규칙은 다음과 같습니다.
- 롤러가 벽에서 떨어지지 않아야 합니다.
- 영역의 일부만 덮도록 칠하지 마십시오.
즉, 롤러의 좌우 끝을 영역의 경계선 또는 벽의 좌우 끝과 정렬한 후 롤러를 위아래로 움직이면서 벽을 쓸어넘기면 된다. 칠할 현재 영역을 완전히 칠한 후 벽에서 롤러를 제거하고 벽에 바릅니다. 한 번 그린 것으로 정의됩니다.
영역을 여러 번 칠하거나 다시 칠할 필요가 없는 영역을 칠할 수 있지만 다시 칠할 영역은 한 번 이상 칠해야 합니다. 비용을 절약하기 위해 재도색이 필요한 영역을 결정한 것처럼 페인트 롤러의 수를 최소화하고자 합니다.
존재들 N, m과 다시 칠할 영역의 수를 포함하는 정수 배열입니다. 섹션이 매개변수로 주어졌을 때 롤러를 칠해야 하는 최소 횟수를 반환하는 솔루션 함수를 작성하세요.
- 1 ≤ 중 ≤ N ≤ 100,000
- 1 ≤ 섹션 길이 ≤ N
- 1 ≤ 섹션 ≤의 요소 N
- 섹션의 요소는 다시 칠해야 하는 섹션의 번호입니다.
- 동일한 요소가 섹션에 두 번 이상 나타날 수 없습니다.
- 섹션의 요소는 오름차순으로 정렬됩니다.
I/O 예시
| N | 중 | 부분 | 결과 |
| 8일 | 4 | (2, 3, 6) | 2 |
| 5 | 4 | (1, 3) | 하나 |
| 4 | 하나 | (1, 2, 3, 4) | 4 |
I/O 예제 #1
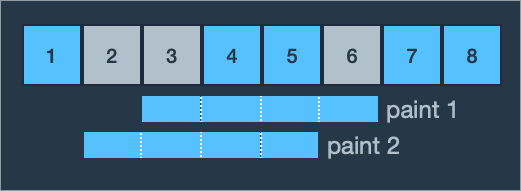
- 예 1에서는 영역 2, 3 및 6을 다시 칠해야 합니다.
- 롤러의 길이가 4미터이기 때문에 한 번에 4면을 연속해서 칠할 수 있습니다.
- 3, 4, 5, 6 영역을 먼저 칠하면 2 영역만 칠할 영역으로 남고, 1, 2, 3, 4 영역을 칠하면 모든 영역을 두 번 다시 칠해야 합니다.
- 2번 미만의 스트로크로 영역 2, 3 및 6을 칠할 방법이 없습니다.
- 따라서 최소 횟수인 2가 반환됩니다.
I/O 예제 #2
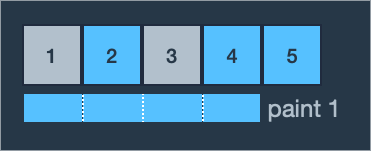
- 예제 #2는 영역 #1과 #3을 다시 칠해야 합니다.
- 롤러의 길이가 3미터이기 때문에 1교대로 연속된 3개 영역을 칠할 수 있고, 1, 2, 3 영역을 칠하면 1, 3영역을 한번에 칠할 수 있습니다.
- 따라서 최소 횟수인 1이 반환됩니다.
I/O 예제 #3
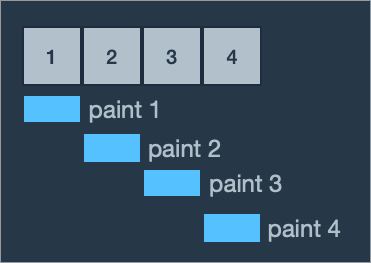
- 예 3에서는 모든 영역을 칠해야 합니다.
- 롤러의 길이가 1미터이기 때문에 한 번에 한 영역만 칠할 수 있습니다.
- 영역이 4개이므로 최소 횟수는 4이며 각 영역은 한 번만 칠합니다.
- 따라서 4를 반환합니다.
내 코드
class Solution {
public int solution(int n, int m, int() section) {
int answer = 0;
int() wall = new int(n+1);
for(int i=0; i<section.length; i++) wall(section(i)) = 1;
for(int i=1; i<wall.length; i++) {
// 해당 벽을 칠해야 하는 경우
if(wall(i) == 1) {
int end = i + m > n + 1 ? n + 1 : i + m;
for(int j=i; j<end; j++) wall(j) = 0;
answer++;
}
}
// 간단한 풀이
// int painted = 0;
// for(int i=0; i<section.length; i++) {
// if(painted < section(i)) {
// painted = section(i) + m - 1;
// answer++;
// }
// }
return answer;
}
}
설명
- int 배열 벽을 만들고 페인팅이 필요한 영역을 1로, 나머지는 0으로 초기화합니다.
- 이제 벽을 횡단하면서 칠해야 하는 영역의 경우(Wall(i) == 1) m 영역의 벽은 해당 영역만큼 0으로 변경되고, 답은 1씩 증가합니다. 그린. (i+m이 벽의 범위를 벗어나면 범위를 마지막 범위로 설정합니다.)
- 미니멀한 페인팅 케이스가 리스폰스로 저장되었으므로 리스폰스는 그대로 리턴됩니다.
간단한 해결책
- 그려진 영역까지 저장하도록 painted를 선언하고 0으로 초기화합니다.
- 도색이 필요한 구간을 순회할 때 해당 영역이 도색보다 크면 도색을 해야 하므로 답은 1씩 증가하고 도색은 해당 구간 + m – 1로 변경된다. (구간을 포함하여 m개이므로 -1로 설정하여 해당 구간을 포함하여 m까지 칠한 부분이 되도록 해야 합니다.)
- 마지막으로 응답은 색상이 필요할 때마다 증가하기 때문에 그대로 반환됩니다.